
电磁感应等距有外力双杆模型概述
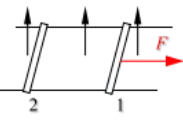
如图所示,光滑水平平行金属轨道,间距为L,金属杆1、2的质量分别为m1、m2,电阻分别为R1、R2,匀强磁场B与导轨平面垂直。金属杆1在恒力F作用下从静止向右运动,讨论因两个杆的运动引发的物理问题。这类问题称为等距有外力双杆模型。
情景过程分析
(1)电路问题分析
杆1相当于电源,杆2受安培力而加速起动,运动后产生反电动势,如图示。两杆电动势叠加后电路中形成电流。
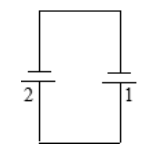
(2)动力学分析:
运动性质分析,四步分析法:①某时刻杆1的速度为v1、杆2的速度为v2,电动势为E=BLv1-BLv2;
②电路中的电流![]()
③两杆受到的安培力![]()
杆1加速度大小:![]()
杆2加速度大小: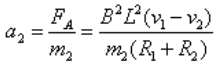
对双杆运动过程的讨论
在最初阶段,安培力FA很小,所以a1>>a2,导致v1–v2不断增大,由以上加速度表达式可知,杆1的加速度a1减小,杆2的加速度a2增大,当a2=a1时,则两杆速度差v2–v1恒定,导轨中的电流I恒定,安培力FA恒定,之后两个杆开始以相同的加速度做匀加速直线运动。
由以上分析可知,杆1做加速度减小的加速运动,然后做匀加速直线运动,杆2做加速度增大的加速运动,然后做匀加速直线运动,速度—时间图象如图示。
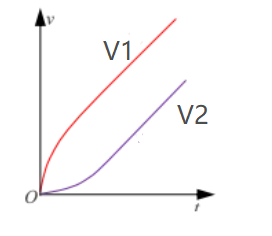
根据上面四部分析可知,求解速度差值,关建是求解稳定状态的加速度。利用整体法,在稳定状态下对两杆利用牛顿第二定律有:F=(m1+m2)a
结合任意一个杆的加速度表达式,联立解得: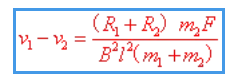
点悟:抓住处理问题的关键方法——四步分析法(源、流、力、加),分析运动性子和求解速度差这些较难问题经变得十分清晰,降低难度。
等距有外力双杆模型动量分析
(1)动量守恒定律的应用:两杆运动过程中,系统受外力F,动量不守恒。
(2)动量定理应用:对杆1杆:Ft-I安=m1v1
对杆2杆:I安=m2v2
对系统:Ft=m1v1+m2v2
不难发现,结合速度差值表达式,可以求解当两杆达到稳定状态外力F的作用时间t。
等距有外力双杆模型能量分析
由功能关系可得:![]()
例题:
1、如图,平行光滑金属导轨M、N固定在水平面上,处于竖直向下的匀强磁场中.完全相同的两金属棒P、Q搭放在导轨上,开 始均处于静止状态.给P施加一与导轨平行的恒定拉力作用,运动中两 金属棒始终与导轨垂直并与导轨接触良好,设导轨足够长,除两棒的电 阻外其余电阻均不计.则两棒的速度及棒中的感应电流随时间变化的图 象正确的是( )
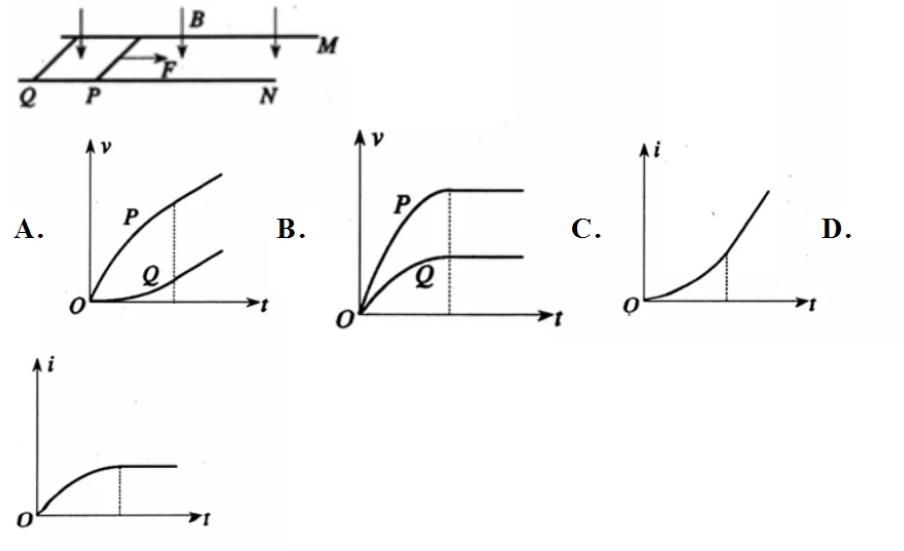
[解析] P向右做切割磁感线运动,由右手定则判断知,回路中产生逆时针的感应电流,由左手定则判断可知,Q棒所受的安培力方向向右,故Q向右做加速运动; Q向右运动后,开始阶段,两杆的速度差增大,产生回路中产生的感应电动势增大,感应电流增大,两杆所受的安培力都增大,则P的加速度减小,Q的加速度增大,当两者的加速度相等时, .速度之差不变,感应电流不变,安培力不变,两杆均做加速度相同的匀加速运动. AB、开始运动时,P棒做加速度减小的加速度运动,Q棒做加速度增大的加速运动,最终做加速度相同的加速度运动,故A正确,B错误; CD、开始运动时,两棒的速度差增大,感应电动势增大,通过电流增大,最终两棒都做匀加速运动,速度差保持不变,故回路中感应电动势不变,电流恒定,故C错误,D正确.故选AD.
2、如图所示,间距为L、电阻不计的足够长双斜面型平行导轨,左导轨光滑,右导轨粗糙,左、 右导轨分别与水平面成a、β角,分别有垂直于导轨斜面向,上的磁感应强度为B1、B2的匀强磁场,两处的磁场互不影响.质量为m、电阻均为r的导体棒ab、cd与两平行导轨垂直放置且接触良好. ab棒由静止释放,cd棒始终静止不动.求:
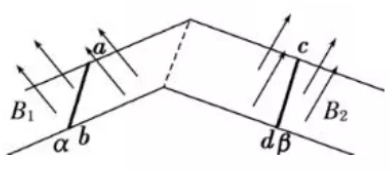
(1) ab棒速度大小为v时通过cd棒的电流大小和cd棒受到的摩擦力大小.
(2) ab棒匀速运动时速度大小及此时cd棒消耗的电功率.


本文作者:徐建强。微信公众号:高中物理学习研究
高中物理知识点总结
发表回复
要发表评论,您必须先登录。