点击观看初、高中名师课程
万有引力定律在考试中有一个对同学们来说比较难的模型——双星、三星模型，这也是考试的重点和难点。
万有引力定律之双星模型
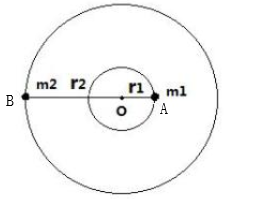
双星模型示意图
如上图所示，质量分别为m1、m2的双星A和绕同中心点O做匀速圆周运动，其中行星A到O点的距离为r1，行星B到O点的距离为r2，设它们的角速度为w。
分析：既然行星A、B都是做匀速圆周运动，那肯定有力提供它们做圆周运动的向心力，这个力只能是它们之间的万有引力，所以根据万有引力提供向心力可得
对行星A：
对行星B：
联立两式可知
以上是双星模型中最核心的两个等式，也是同学们最容易列错的等式，因为在这里万有引力的引力半径不等于天体做圆周运动的轨道半径，双星模型中行星的周期和角速度相等。
列出了这两个等式，不管题目怎么变，根据题意联立带值就行，一种很常见的题目就是已知r1、r2、T，要你求m1+m2，列出上面两个等式就很容易得出。
万有引力定律之三星模型
三星模型是指由三个行星组成的稳定三星系统，忽略其他行星对其影响，一般有两种形式。
1、三颗行星在一条直线上，其中有两颗行星绕第三个行星在同一轨道半径R上做匀速圆周运动，如下图。
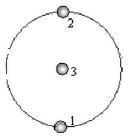
设其中两行星的轨道半径为R，三颗行星的质量都为m。
分析：整个解题过程还是一样，始终抓住万有引力提供向心力，如果多个万有引力提供向心力，那么把多个万有引力进行矢量合成，合力提供向心力，三星模型很明显对于一个行星来说，会受到另外两行星对它的万有引力，所以得将这两个万有引力进行合成，合成以后的力提供向心力。
对行星1：
(等式左边为行星3、行星2对行星1万有引力的合力)
可解的：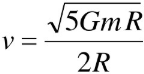
周期
2、三颗行星位于等边三角形的三个顶点上，运动轨迹为这个三角形的外接圆，如下图。
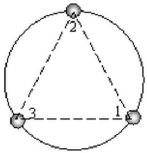
设三颗行星的质量都为m，外接圆的半径为R。
分析：三颗行星都在做匀速圆周运动，做圆周运动的向心力由另外两个行星对其万有引力的合力提供。
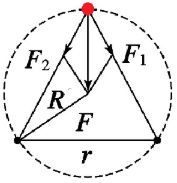
对行星2受力分析示意图
由几何关系可得
F1、F2的合力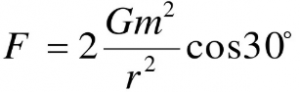
合力提供向心力
，这样就可以得出运动的周期T，周期T解出，运动的速度也可以得出。
双星、三星模型可以解，四星、五星模型也是一样解，始终抓住万有引力提供向心力，如果一个行星受到多个行星对它的万有引力，那么就进行矢量合成，合成后的万有引力提供向心力。
双星模型、三星模型练习下载
高中物理知识点总结
2 comments